83. Conectividad gráfica
Autor: Mauricio Nina Canaviri
Limite de tiempo : 1 seg. Total runs : 5 Aceptados : 3
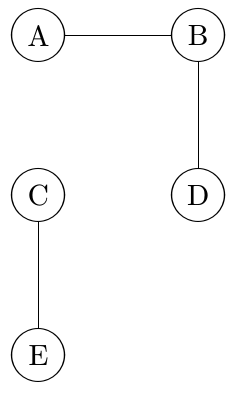
Considere un gráfico G formado a partir de un gran número de nodos conectados por los bordes. G se dice que está conectado si se puede encontrar una ruta en 0 o más pasos entre cualquier par de nodos en G. Por ejemplo, el gráfico de abajo no está conectado porque no hay ruta de A a C.
Este gráfico contiene, sin embargo, un número de subgrafos que están conectados, uno para cada uno de los siguientes conjuntos de nodos: {A}, {B}, {C}, {D}, {E}, {A,B}, {B,D}, {C,E}, {A,B,D}.
Un subgrafo conectado es máximo si no hay nodos y aristas en el gráfico original que se podrían agregar al subgrafo y aún así dejarlo conectado.
Hay dos subgrafos conectados máximos arriba, uno asociado con los nodos {A, B, D} y el otro con los nodos {C, E}.
Escriba un programa para determinar el número de subgrafos conectados máximos de un grafo dad
Entrada
La entrada comienza con un solo entero positivo en una línea por sí mismo que indica el número de los casos siguientes, cada uno de ellos como se describe a continuación. Esta línea es seguida por una línea en blanco, y también hay una línea en blanco entre dos entradas consecutivas.
La primera línea de cada conjunto de entrada contiene un solo carácter alfabético mayúsculo. Este carácter representa el nombre de nodo más grande del gráfico.
Cada línea sucesiva contiene un par de caracteres alfabéticos mayúsculos que denotan un borde en el gráfico. La sección de entrada de muestra contiene un posible conjunto de entrada para la gráfica mostrada arriba.
La entrada se termina con una línea en blanco
Salida
Para cada caso de prueba, escriba en la salida el número máximo de subgrafos conectados.
Las salidas de dos casos consecutivos estarán separadas por una línea en blanco.
Ejemplo Entrada
2
E
AB
CE
DB
CE
B
AB
Ejemplo Salida
2
1Algo anda mal: